Analyzing a steganography software:

InPlainView

     1. Background

These last few days I had fun having a look at very simple steganography software which simply adds the "hidden" data at the end of carrier files, like Camouflage and JpegX. Both of them were easily breakable, and offer an extremely weak security. But security, of course, is just a relative concept, dependant on the importance of your data, or more precisely, in the case of steganography, the importance that nobody discovers that you are hiding data. So, Camouflage or JpegX may be enough if you just want to hide the addresses of a few porn sites from the eyes of your grand-mother.

Today I checked another program called InPlainView, which uses a more traditional approach of hiding data inside an image, by modifying the Low Significance Bits (LSB) of each pixel. In an uncompressed 24-bit BMP file, there is no palette or color table, and right after the BMP header, you have the raw pixel data. For each pixel you have one byte for the Blue saturation value (8-bits, so 256 values), same for Green, and then for Red. Hence each pixel needs 3x8 = 24 bits, and can take 256x256x256 colors, so around 16 millions.

If you modify the LSB for each pixel (incrementing or decrementing it), you won't change the Blue, Green, Red components of this pixel more than 1/256th. So it's not visible to the naked eye.

     2. Simple LSB is not enough

What is not visible by eye can be easily visible for a software. Or the software can extract data from the noise, until it's visible by naked eye. InPlainView hides the bit stream starting with the first pixel, and the next ones until it does not have anything more to hide. That creates an easily recognizable pattern at the beginning of the file (remember for later: BMP files are encoded upside-down), even if the hidden text is totally random, or heavily encrypted. So, we can say that's it's easy to notice there is something hidden in the file.

Here is an example of a steganographical visual attack. I like it, because it's really intuitive. The idea came after reading some work by Andreas Westfeld. The concept behind this is that LSBs in an image are not random, unlike most people think. If you change them in a simple way, an attacker will know it.

I quickly coded a small utility that does almost the opposite of steganography softwares: it eliminates all information from a 24-bit BMP except the LSB, and then enhances it (if LSB is 1, the whole byte becomes 1, so we can see some flashy colors). Let's check it with a photo of Audrey Hepburn found on the Net, with or without a hidden message (the poem "If" by Rudyard Kipling, in three languages) which length is a little bit less than half of the maximal capacity of the image. Of course, because we are on the web, I had to retransform the BMP into GIF or JPG. The steganography is done with InPlainView.

This is the original image. With or without hidden text, it would look the same to the naked eye. And Audrey Hepburn looks really great, naked eye or not.	This are just the enhanced LSBs of the original image without any text. Not really random as we can see.	This are the enhanced LSBs of the image containing the hidden text. You can clearly see the hidden text as a distinct pattern on the bottom of the image. Suddenly not that hidden, heh?

Another example with a more "normal" image (what is a "normal" image anyway?).

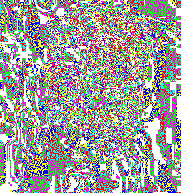
This is the original image.	This are the enhanced LSBs of the original image.	This are the enhanced LSBs of the image containing the hidden text. Once again it's pretty visually evident. A statistical analysis on this stream could be done to automatize the task.

     3. Back to InPlainView

So we now know that it's easy to detect a LSB stream of hidden data. Let's look specifically at the inner workings of InPlainView software. Just before the hidden text, it writes 5 bytes, which may be a kind of signature. This is a bad idea, because a signature means that an attacker can use it to detect the presence of data, too.

This signature consists in:

     - 2 bytes at zero.
     - 2 bytes containing the size of the hidden text.
     - 1 byte containing 0 if no password is used, 1 if there is a password.

The encryption is a simple XOR of the password (repeated as many times needed) with the text. The strength of this encryption can go from very low to extremely high. It actually totally depends on two variables:

     => the password size compared to the text size.
     => the randomness of the text (normal text has some very recognizable patterns) and the password.

With a random password the same size than the text, it's similar to a One Time Pad, and it's the only encryption method proven to be absolutely unbreakable. With a short password and a very long normal text, it can be cracked in a minute.

Because the author of this software does not explain how it works, and does not stress the importance of a very long random password in this type of encryption, you can bet that most of the people are going to use unsecure passwords. That's why I consider the global level of this software, cryptographically speaking, as "Medium". Which does not mean anything. But who cares, I'm not a specialist anyway, I'm just having fun :)

     4. My InPlainView Test Extractor

I rapidly coded a small software called "InPlainView Hidden Text Finder", with source. Here is what it's doing:

=> if the file is not a 24-bits BMP, it says so and stops
=> if the 5 first bytes of hidden data do not look like a InPlainView hidden text header, it says so and stops
=> if the hidden text is not encrypted, it's displayed on a MessageBox
=> if the hidden text is encrypted, it's saved as a raw binary file for you to analyze later, called "hidden_encrypted.bin"

     5. An example of how to break an encrypted file

This is no more related to steganography, but more to the basical principes of good old grandma frequency analysis. But it's still fun, so here we go. A simple example, to go fast.

My enemy hides the "If" poem in some image with InPlainView. He uses the simple password "zobi", and send this image somewhere by email.

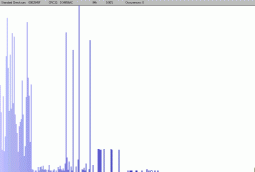
I intercept the email, and curious as I am, I see that there is some hidden data, compatible with InPlainView style, and want to find out. My Extractor tells me there is a password, so I save the raw encrypted data. I then look at the byte distribution spectrum of this data, with the help of the truely excellent WinHex editor. It looks like this:

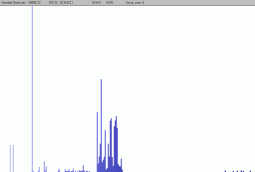
This is the distribution frequence spectrum of the bytes in the encrypted "If" file. Notice the differences compared to the typical spectrum on the right. Signature peaks are cut in 4 pieces, they are wider and more blurred, and everything is shifted.	Just for the record, this is the spectrum of the original text file. The two exactly equal small bar on the left are 0Dh and 0Ah, values for line breaks. Then you have the tall "space" bar, and then the block of values used for actual letters. Written text has a unique signature, even more precise if you consider a unique language like french or english.

Have a nice day!


     Guillermito, September 21th 2002